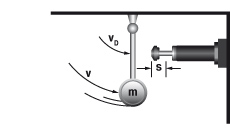
It is easy to calculate around 90 % of applications knowing only the following five parameters:
- Mass to be decelerated (weight) m [kg]
- Impact velocity at shock absorber vD [m/s]
- Propelling force F [N]
- Cycles per hour c [1/h]
- Number of absorbers in parallel n
Key to symbols used
| Symbol | Unit | Description | Symbol | Unit | Description |
|---|---|---|---|---|---|
| W1 | Nm | Kinetic energy per cycle | 3ST | 1 to 3 | tall torque factor (normally 2.5) |
| W2 | Nm | Propelling force energy per cycle | M | Nm | Propelling torque |
| W3 | Nm | Total energy per cycle (W1 + W2) | I | kgm2 | Moment of Inertia |
| 1W4 | Nm/hr | Total energy per hour (W3 · c) | g | m/s2 | Acceleration due to gravity = 9.81 |
| me | kg | Effective weight | h | m | Drop height excl. shock absorber stroke |
| m | kg | Mass to be decelerated | s | m | Shock absorber stroke |
| n | Number of shock absorbers (in parallel) | L/R/r | m | Radius | |
| 2v | m/s | Velocity at impact | Q | N | Reaction force |
| 2vD | m/s | Impact velocity at shock absorber | μ | Coefficient of friction | |
| ω | rad/s | Angular velocity at impact | t | s | Deceleration time |
| F | N | Propelling force | a | m/s2 | Deceleration |
| c | 1/hr | Cycles per hour | α | ° | Side load angle |
| P | kW | Motor power | β | ° | Angle of incline |
Note:
When using several shock absorbers in parallel, the values (W3), (W4) and (me) are divided according to the number of units used.
Reaction force Q [N] Q = (1.5 · W3) / s | Stopping time t [s] t = (2.6 · s) / vD | Deceleration a [m/s2] a = (0.75 · vD2) / s |
Applications
| Application | Formulae | Example | |
|---|---|---|---|
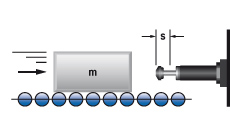
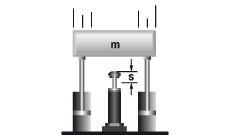
1. Mass without propelling force
| W1 = m · v2 · 0.5 W2 = 0 W3 = W1 + W2 W4 = W3 · c vD = v me = m | m = 100 kg W1 = 100 · 1.52 · 0.5 = 113 Nm | |
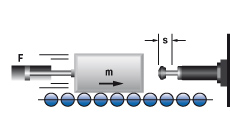
2. Mass with propelling force
| W1 = m · v2 · 0.5 W2 = F · s W3 = W1 + W2 W4 = W3 · c vD = v me = (2 · W3) / vD2 2.1 for vertical motion upwards W2 = (F – m · g) · s 2.2 for vertical motion downwards W2 = (F + m · g) · s | m = 36 kg 1v = 1.5 m/s F = 400 N c = 1000 1/hr s = 0.025 m (chosen) W1 = 36 · 1.52 · 0.5 = 41 Nm W2 = 400 · 0.025 = 10 Nm W3 = 41 + 10 = 51 Nm W4 = 51 · 1000 = 51000 Nm/hr me = 2 · 51 : 1.52 = 45 kg 1 v is the fi nal impact velocity of the mass: With pneumaticallypropelled systems this can be 1.5 to 2 times the average velocity. Please take this into account when calculating energy. | |
3. Mass with motor drive
| W1 = m · v2 · 0.5 W2 = (1000 · P ·ST · s) / v W3 = W1 + W2 W4 = W3 · c vD = v me = (2 · W3) / vD2 | m = 800 kg W1 = 800 · 1.22 · 0.5 = 576 Nm motor, coupling and gearbox into calculation for W1. | |
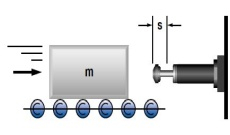
4. Mass on driven rollers
| W1 = m · v2 · 0.5 W2 = m · μ · g · s W3 = W1 + W2 W4 = W3 · c vD = v me = (2 · W3) / vD2 | m = 250 kg W1 = 250 · 1.52 · 0.5 = 281 Nm | |
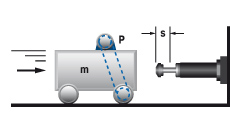
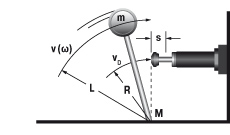
5. Swinging mass with propelling force
| W1 = m · v2 · 0.5 = 0.5 · I · ω2 W2 = (M · s) / R W3 = W1 + W2 W4 = W3 · c vD = (v · R) / L = ω · R me = (2 · W3) / vD2 | m = 20 kg W1 = 20 · 12 · 0.5 = 10 Nm | |
6. Free falling mass
| W1 = m · g · h W2 = m · g · s W3 = W1 + W2 W4 = W3 · c vD = √2 · g · h me = (2 · W3) / vD2 | m = 30 kg W1 = 30 · 0.5 · 9.81 = 147 Nm | |
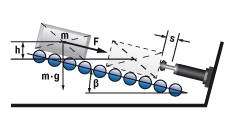
6.1 Mass rolling/sliding down incline
| W1 = m · g · h = m · vD2 · 0.5 W2 = m · g · sinβ · s W3 = W1 + W2 W4 = W3 · c vD = √2 · g · h me = (2 · W3) / vD2 6.1a propelling force up incline W2 = (F – m · g· sinβ) · s 6.1b propelling force down incline W2 = (F + m · g· sinβ) · s | m = 500 kg W1 = 500 · 9.81 · 0.1 = 490.5 Nm | |
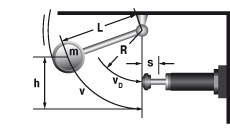
6.2 Mass free falling about a pivot point
| W1 = m · g · h W2 = 0 W3 = W1 + W2 W4 = W3 · c vD = √2 · g · h · (R / L) me = (2 · W3) / vD2 tan α = s / R | m = 50 kg W1 = 50 · 9.81 · 1 = 490.5 Nm | |
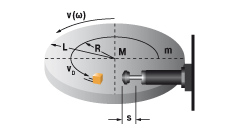
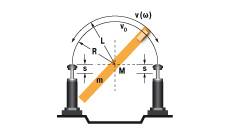
7. Rotary index table with propelling torque
| W1 = m · v2 · 0.25 = 0.5 · I · ω2 W2 = (M · s) / R W3 = W1 + W2 W4 = W3 · c vD = (v · R) / L = ω · R me = (2 · W3) / vD2 | m = 1000 kg W1 = 1000 · 1.12 · 0.25 = 303 Nm | |
8. Swinging arm with propelling torque | W1 = m · v2 · 0.17 = 0,5 · I · ω2 W2 = (M · s) / R W3 = W1 + W2 W4 = W3 · c vD = (v · R) / L = ω · R me = (2 · W3) / vD2 | I = 56 kgm2 W1 = 0.5 · 56 · 12 = 28 Nm | |
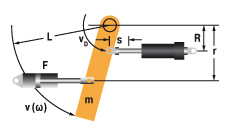
9. Swinging arm with propelling force | W1 = m · v2 · 0.17 = 0.5 · I · ω2 W2 = (F · r · s) / R = (M · s) / R W3 = W1 + W2 W4 = W3 · c vD = (v · R) / L = ω · R me = (2 · W3) / vD2 | m = 1000 kg W1 = 1000 · 22 · 0.17 = 680 Nm | |
10. Mass lowered at controlled speed
| W1 =m · v2 · 0.5 W2 = m · g · s W3 = W1 + W2 W4 = W3 · c vD = v me = (2 · W3) / vD2 | m = 6000 kg W1 = 6000 · 1.52 · 0.5 = 6750 Nm | |
Use calculation tool and order online
Effective Weight (me)
The effective weight (me) can either be the same as the actual weight (examples Aand C), or it can be an imaginary weight representing a combination of the propelling force or lever action plus the actual weight (examples B and D).
| Einsatzfall | Beispiel |
|---|---|
A Mass without propelling force
| m = 100 kg vD = v = 2 m/s W1 = W3 = 200 Nm me = (2 · 200) / 4 = 100 kg Formula: me = m |
B Mass with propelling force
| m = 100 kg F = 2000 N vD = v = 2 m/s s = 0.1 m W1 = 200 Nm W2 = 200 Nm W3 = 400 Nm me = (2 · 400) / 4 = 200 kg Formula: me = (2 · W3) / vD2 |
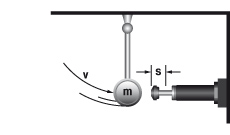
C Mass without propelling force direct | m = 20 kg vD = v = 2 m/s W1 = W3 = 40 Nm me = (2 · 40) / 22 = 20 kg Formula: me = m |
D Mass without propelling force with | m = 20 kg v = 2 m/s vD = 0.5 m/s s = 0.1 m W1 = W3 = 40 Nm me = (2 · 40) / 0.52 = 320 kg Formula: me = (2 · W3) / vD2 |